Geometria Plana
A geometria plana, também chamada geometria elementar ou Euclidiana, teve início na Grécia antiga. Esse estudo analisa as diferentes formas de objetos, e baseia-se em três conceitos básicos: ponto, reta e plano.
O conceito de ponto é primitivo, pois não existe uma definição aceita de ponto. Temos, entretanto, que aceitar sua existência e indicamos um ponto por uma letra maiúscula do alfabeto (A, G, P,. . . ).
Podemos definir uma reta como um número infinito de pontos em sequência. Não é difícil perceber que sobre um ponto passa um número infinito de retas, porém sobre dois pontos distintos passa apenas uma reta distinta. Uma reta que passe por estes dois pontos é chamada de reta infinita. Caso ela comece em um ponto qualquer e não tenha fim, é denominada reta semi-infinita. Já no caso de se iniciar em um ponto e terminar em um outro, é denominada semi-reta. Indicamos uma reta por uma letra minúscula qualquer (r,s,t,. . . ).
Para relacionarmos no espaço as retas entre si temos que saber quais suas posições relativas, o que pode ser feito usando-se a definição de ângulo: O ângulo geométrico é dado pela união de duas retas não colineares (que estão na mesma linha) partindo da mesma origem. O ângulo entre estas duas retas é medido em graus, de tal forma que caibam 180° em uma circunferência completa.
Exercícios
1) Temos um triângulo equilátero de lado 6cm. Qual é o perímetro e qual é a área deste triângulo?
Solução:
- Perímetro:
6*3 = 18cm
- Área:
![]()
2) Um trapézio tem a base menor igual a 2, a base maior igual a 3 e a altura igual a 10. Qual a área deste trapézio?
Solução:
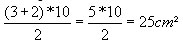
3) Sabendo que a área de um quadrado é 36cm², qual é seu perímetro?
Solução:
Vamos descobrir o lado do quadrado:
x*x = 36
x = ![]()
x = 6
Agora é só achar o perímetro:
x= 6.4
X = 24
